10-1-4有向圖形
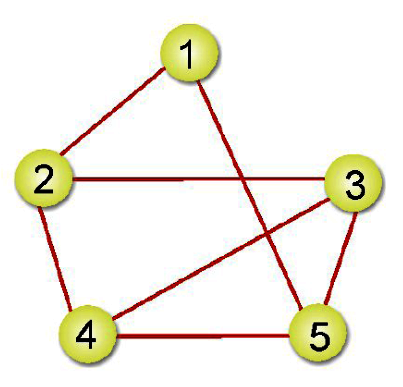
有向圖形(Digrph)是一種每一個邊都可使用有序對<V1,V2>來表示,並且<V1,V2>與<V2,V1>是表示方向不同的邊,而所謂<V1,V2>,是指V1為尾端指向為頭部的V2。如下圖所示:
V={A,B,C,D,E}
E={<A,B>、<B,C>、<C,D>、<C,E>、<E,D>、<D,B>}
接下來則是有向圖形的相關定義介紹:
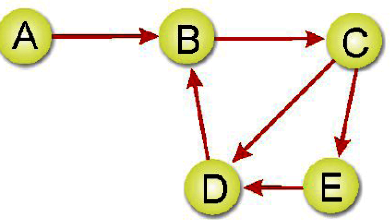
*完整圖形(Complete Graph):具有n個頂點且恰有n*(n-1)個邊的有向圖形,如下圖所示:
*路徑(Path):有向圖形中從頂點Vp到頂點Vq的路徑是指一串由頂點所組成的連續有像序列。
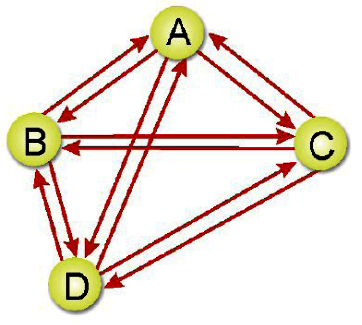
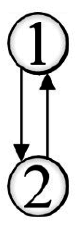
*強連接(Strongly Connected):有向圖形中,如果每個相異的成對頂點Vi,Vj有直接路徑,同時,有另一條路徑從Vj到Vi,則稱此圖為強連接。如下圖:

*強連接單元(Strong Connected Component):有向圖形中構成強連接的最大子圖,在下圖(A)中是強連接,但(B)就不是。
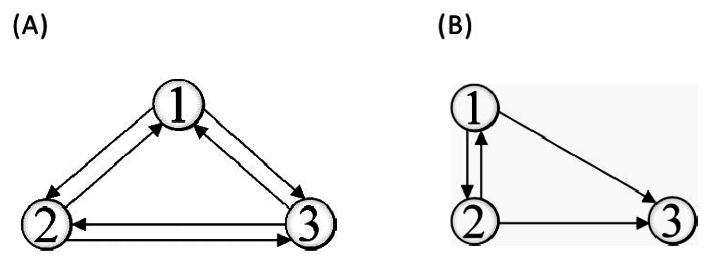
而圖(B)中的強連接單元如下:
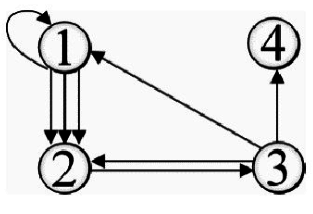
*出分支度(Out-degree):是指有向圖形中,以頂點V為劍尾的邊數目。
*入分支度(In-degree):是指有向圖形中,以頂點V為箭頭的邊數目,下圖中V4的入分支度為1,出分支度為0,V2的入分支度為4,出分支度為1。
10-2不能不學的圖形表示法
知道圖形的各種定義與觀念後,有關圖形的資料表示法就易顯重要了。常用來表達圖形資料結構的方法很多,本節中將介紹四種表示法。
10-2-1相鄰矩陣法
圖形A有n個頂點,以n*n的二為矩陣陣列表示。此矩陣的定義如下:

相關特性說明如下:

接著就實際來看一個範例,請以相鄰矩陣表示右邊的無向圖:由於下圖共有5個頂點,故使用5*5的二維陣列存放圖形。下圖中,先找和1相鄰的頂點有哪些,把和1相鄰的頂點座標填入1。